প্রদীপ কুমার মজুমদার 
ব্রহ্মগুপ্ত, মহাবীর, দ্বিতীয় আর্যভট, দ্বিতীয় ভাস্করাচার্য প্রমুখের প্রণালীতে সমাধান করে এদের পদ্ধতিগুলি স্পষ্ট করে তুলে ধরছি…
পার্থক্য (ক) পরিবর্তিত ৫=by+c এর প্রথম পদ্ধতির সমাধান প্রথম আর্যভট ও দ্বিতীয় ভাস্করাচার্যের মধ্যে পার্থক্য বর্তমান। যদিও ভাগশেষের শৃঙ্খলটি দ্বিতীয় ভাস্করাচার্য প্রথম আধভটের শৃঙ্খল থেকে সাহায্য নিয়েছেন। এখন প্রথম আর্যভট, দ্বিতীয় আর্যভট ও দ্বিতীয় ভাস্করাচার্যের ভাগশেষের শৃঙ্খল নিয়ে তুলনা করা যাক।
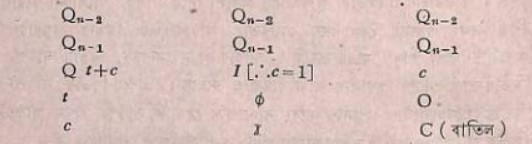
দ্বিতীয় ভাস্করাচার্য অতিরিক্ত হেতু বাতিল করে দিয়েছেন, দ্বিতীয় আর্যভট ঐ একই কারণে এবং 1 কে বাতিল করে দিয়েছেন।
(খ) দ্বিতীয় ভাস্করাচার্য ক্ষেপ ঋণাত্মক হলে এবং ভাজক দ্বারা বিভাজ্য হলে সেক্ষেত্রে বাতিল করেন নি।
Ax = By – mA সমীকরণে যখন y = 0 ধরেছেন। x = – m
x = Bt – m y = At এবং এর এমন একটি সাংগিক মান দিয়েছেন যার ফলে ধনাত্মক হয়। এছাড়াও আরও নানা পার্থক্য লক্ষ্য করা যায়।
এখন আমরা অনির্ণেয় সমীকরণের একটি উদাহরণ 63x = 100y + 90 নিয়ে প্রথম আর্যভট, ব্রহ্মগুপ্ত, মহাবীর, দ্বিতীয় আর্যভট, দ্বিতীয় ভাস্করাচার্য প্রমুখের প্রণালীতে সমাধান করে এদের পদ্ধতিগুলি স্পষ্ট করে তুলে ধরছি।
(ক) প্রথম আর্যভট
এ ক্ষেত্রে আর্যভটের শৃঙ্খলগুলি নিম্নরূপ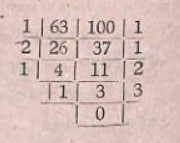 
1 -> 100t + 2430
1 -> (37t + 900) + (26t + 630) = 63t + 1530
1 -> (26t + 630) + (11t + 270) = 37t + 900
2 -> (11t + 270) + (4t + 90) = 26t + 630
2 -> 2(4t + 90) + (3t + 9t) = 11t + 270
1 -> (3t + 90) + t = 4t + 90
3 -> 3t + 90
t
90
এখন 63t +1530 ≡ 8(mod 63)
y এর লঘিষ্ট মান y = 18
আবার 100t +2430≡ 30(mod 100)
x এর লঘিষ্ট মান x = 30
(চলবে)
