প্রদীপ কুমার মজুমদার 
প্রত্যেক স্তরে ২১টি ইট থাকবে। ইটগুলি বর্গীকার, আয়তাকার বা যে কোন আকৃতি বিশিষ্ট হতে পারে।
নানা ধরণের যজ্ঞবেদী নির্মাণ পদ্ধতি ভারতীয় ঋষিরা জানতেন। এবং এই সবক্ষেত্রে উন্নত পর্যায়ের বীজগণিতের প্রয়োগ লক্ষ্য করা যায়। মহাবেদী নির্মাণ করতে গিয়ে দেখা গিয়েছে একটি সমদ্বিবাহু ট্রাপিজিয়ম যার সম্মুখভাগ ২৪ একক দীর্ঘ, ভূমি ৩০একক, উচ্চতা ৩৬ একক এবং একক করে আকৃতি বৃদ্ধি করলে m একক ক্ষেত্রের জন্য আমরা নিম্নলিখিত বীজগণিতীয় সমীকরণটি পাই
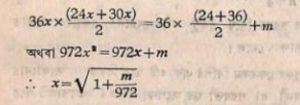
যদি m = 972(n – 1) বসান যায় তাহলে √n পাওয়া যায় 1 < n = 14 বা 143 শতপথ ব্রাহ্মণে পাওয়া যায়।
শোণচিত নির্মাণ করতে গিয়ে আমরা নিম্নলিখিত বীজগণিতীয় সমীকরণের সাক্ষাৎ পাই (অবশ্য আধুনিক বীজগণিতে রূপ দেবার পর)
m = অগ্নিবেদীর আকৃতি বৃদ্ধি ধরা হয়েছে।
তাহলে x ²= 1 + (nm)/15m m = 94 ধরলে x ² = 13 1/15 = 14 (আসন্ন) ফল পাওয়া যাবে এবং এটি শতপথ ব্রাহ্মণে দেখতে পাওয়া যায় 3 ?
শুবস্থত্র নির্দিষ্ট আকৃতি বিশিষ্ট যজ্ঞবেদী নির্মাণ করতে গিয়ে অনেকবর্ণ অনির্ণেয় সমীকরণ (Indeterminate equations in several variables) দেখতে পাওয়া যায়। “গার্হপত্যয় বেদী” নির্মাণ কল্পে বলা হয়েছে, একটি বর্গক্ষেত্র যার বাহু ১ ব্যায়ম এবং ৫টি স্তর ইট দিয়ে তৈরী। প্রত্যেক স্তরে ২১টি ইট থাকবে। ইটগুলি বর্গীকার, আয়তাকার বা যে কোন আকৃতি বিশিষ্ট হতে পারে। কিন্তু পরপর দুটি স্তরের ইটগুলির ফাঁক এক লাইনে পড়বে না।
ধরা যাক ইটগুলি বর্গাকার, তিন ধরণের ইট পাওয়া যাবে যাদের বাহু উও ও ব্যায়ম। প্রথম স্তরটি ব্যায়ম দৈর্ঘ্য বিশিষ্ট ১টি ইট এবং ব্যায়ম দৈর্ঘ্য বিশিষ্ট ১২ ইট থাকবে। দ্বিতীয় স্তরে উ ব্যায়ম দৈর্ঘ্য বিশিষ্ট ১৬টি ইট এবং উ ব্যায়ম দৈর্ঘ্য বিশিষ্ট ৫টি ইট থাকবে।
(চলবে)
