প্রদীপ কুমার মজুমদার 
তারপর অজ্ঞাতরাশির সহগের বর্গ যোগ কর। (এই যোগফলের) মূল কত তারপর অজ্ঞাত রাশির সহগ বিয়োগ দাও…..
স্পষ্টই বোঝা যাচ্ছে এটি একটি সুদ কষার অঙ্ক। শ্লোকটির মর্মার্থ আধুনিক গণিতের ভাষায় বললে এরকম হয় প্রতি ৫ টাকায় সূদ এবং মাসে সূদ সহ সমগ্র টাকা এ হলে তাহলে 
এবং
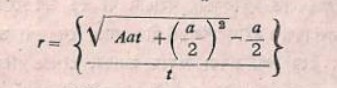
ব্রহ্মগুপ্ত ব্রাহ্মস্ফুট সিদ্ধান্তের অষ্টাদশ অধ্যায়ের ৪৪-তম শ্লোকে বলেছেন-
“বর্গচতুর্ভণিতানাং রূপনাং মধ্যবর্গসহিতানাম্।
মূলং মধ্যেনোনং বর্গদ্বিগুণোদ্ভূতং মধ্যঃ।”
অর্থাৎ অজ্ঞাতরাশির বর্গের সহগের চার গুণের সঙ্গে পরমমান গুণ কর। তারপর অজ্ঞাতরাশির সহগের বর্গ যোগ কর। (এই যোগফলের) মূল কত তারপর অজ্ঞাত রাশির সহগ বিয়োগ দাও। অতঃপর অজ্ঞাতরাশির বর্গের সহগের দ্বিগুণিত দিয়ে ভাগ দাও।
অর্থাৎ ax²+bx=c হলে
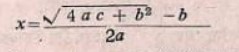
ব্রহ্মগুপ্ত (অষ্টাদশ অধ্যায়, ৪৫-তম শ্লোক) অন্যত্র বলেছেন
বর্গাহতরূপাণামব্যক্তার্ধ কৃতি সংযুতানাং যত,।
পদমব্যক্তার্ধোনং তত্ত্বৰ্গবিভক্তমবক্তঃ।
আধুনিক বীজগণিতের ভাষায় লেখা হলে এইরূপ হয়
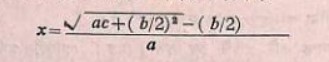
প্রসঙ্গত বলা প্রয়োজন সমান্তর প্রগতির পদ সংখ্যা নির্ণয় করতে গিয়ে ব্রহ্মগুপ্ত প্রথম আর্যভটের ন্যায় সূত্র দিয়েছেন।
(চলবে)
