প্রকোষ্ঠের পাশাপাশা প্রকোষ্ঠদ্বয়ের সংখ্যাছটির যোগফল বসাও। এইভাবে অগ্রসর হও।
এটি এত সংক্ষিপ্ত কিন্তু অত্যন্ত প্রয়োজনীয় কথা যে সাধারণ মানুষ এটির মর্মার্থ বুঝতে পারবে না। এই সংক্ষিপ্ত কথাটির অর্থ হলায়ুধ টীকা করেছেন তিনি বলেছেন:
“অনেন একদ্ব্যাধিলঘুক্রিয়াসিদ্ধার্থং যাবদভিমতং প্রথমপ্রস্তারবত, মেরুপ্রস্তারং দর্শয়তি। উপরিষ্টাদেকং চতুরপ্রকোষ্ঠং লিখিতা তম্ভ্যাধস্তাত, উভয়তোহর্দ্ধনিষ্ক্রান্তং কোর্ডকদ্বয়ং লিখেত,, তন্তাপ্যধস্তাত এয়ং তস্যাপধস্তাচ্চতুষ্টয়মেবং যাবদভিমতং স্থানমিতি মেরুপ্রস্তারঃ। তস্য প্রথমে কোষ্ঠে এক সংখ্যামব্যবস্থাপ্য লক্ষণমিদং প্রবর্ত্তয়েত,। তত্রদ্বিকোষ্ঠায়াং পড়ুক্তাবুভয়োঃ কোষ্ঠয়োরেকৈকমঙ্কং দখ্যাত।
ততত্ত্বতীয়ায়াং পড়ুক্তৌ পৰ্য্যন্ত কোডয়োরেকৈকমংকম্ দক্ষাত,। মধ্যমকোষ্ঠে তুপরিকোষ্ঠহুয়াং কমেকীকৃত্য পূর্ণং নিবশয়েদিতি পূর্ণশব্দার্থঃ। চতু্যাং পঙ্ক্তাবপি পর্য্যন্তকোষ্ঠয়োরে-কৈকমংকম্ স্থাপয়েত। মধ্যমকোষ্ঠয়োও পরিকোষ্ঠদ্বয়াংকমেকীকৃত্য পূর্ণং ত্রিসংখ্যারূপং স্থাপয়েৎ। উত্তরত্রাপ্যেবমেব ন্যাসঃ। তত্র দ্বিকোষ্ঠয়াং পড়ুক্ত বেকাক্ষরশস্য প্রস্তারঃ। তৃতীয়ায়াং পড়ুক্তৌ দ্ব্যক্ষবস্য প্রন্তারঃ। চতুর্থ্যাম পড়ুক্তৌ এ্যক্ষরস্য প্রস্তারঃ।”
এটির সর্মার্থ হচ্ছে-একটি প্রকোষ্ঠ নির্মাণ কর, এটির ঠিক নীচে একই আকারের দুটি প্রকোষ্ঠ নির্মান কর। (ছবি দ্রষ্টব্য) এইরূপে পর পর করে যাও। প্রথম প্রকোষ্ঠে ১ বসাও। এই ভাবে চিহ্ন আরম্ভ হওয়া উচিত (The marking should be started) দ্বিতীয় পঙ্ ক্তির দুটি প্রকোষ্ঠের প্রত্যেকটিতে ১ বসাও। তৃতীয় পক্তির প্রান্ত প্রকোষ্ঠদ্বয়ের প্রত্যেকটিতে ১ বসাও এবং মাছখানের প্রকোষ্ঠটিতে দ্বিতীয় পংক্তিতে অবস্থিত (অবশ্য প্রকোষ্ঠের মধ্যে অবস্থিত) সংখ্যা-দ্বয়ের যোগফল বসাও।
চতুর্থ পড়ুক্তির প্রান্ত প্রকোষ্ঠঘয়ের প্রত্যেকটিতে ১ বসাও মাঝের প্রকোষ্ঠদ্বয়ের প্রত্যেকটিতে তৃতীয় পত্র ক্তিত্ব প্রকোষ্ঠের পাশাপাশা প্রকোষ্ঠদ্বয়ের সংখ্যাছটির যোগফল বসাও। এইভাবে অগ্রসর হও। দ্বিতীয় পংক্তি একটি অক্ষরের সমবায় দেবে। তৃতীয় পঙক্তি দুটি অক্ষরের সমবায় দেবে। ইত্যাদি । এই পদ্ধতিকে “মেরু প্রস্তার” বলে।
এটিকে চিত্রের সাহায্যে উপস্থিত করলে এইরুপ হয়
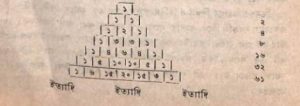
সমবায় সংখ্যা নির্ণয় করতে গেলে প্রথমতঃ একযোগে একটি, দুটি,…… একযোগে সমগ্রগুলি নিয়ে কতগুলি হয় দেখতে হবে। তারপর এগুলির যোগফল নিতে হবে হবে। গাণিতিক সূত্রানুযায়ী বলা যায় nco+ nc1+……+ncn
পিঙ্গলের ছন্দ স্বত্রে আর একটি সূত্র আছে যেটিকে আধুনিক গণিতের ভাষায় লিখলে দাড়ায়
nc1+ ncr+1 = n+1 c r+1
এবার তাহলে স্পষ্টই বোঝা যাচ্ছে পিঙ্গল কেন “পরে পূর্ণমিতি” কথাটি বলেছেন এবং ভাষ্যকার ঠিক উপরের পাশাপাশি প্রকোষ্ঠদ্বয়ের সংখ্যার যোগফল কেন নিতে বলেছেন।
বরাহমিহির মেরু প্রস্তরের নীতিকে সামান্য পরিবর্তন গ্রহণ করেছিলেন। তিনি বৃহৎ সংহিতার এক জায়গায় বলেছেন-
“পূর্ব্বেণ পূর্ব্বেণ গতেন যুক্তং।
স্থানং বিনান্তং সংখ্যাম্।”
কথিত আছে সংখ্যাগুলি পাওয়া যায় যদি প্রত্যেকটির সঙ্গে সম্পূখপূর্ব সংখ্যা যোগ করা যায়। একমাত্র শেষেরটি ছাড়া।
(চলবে)
প্রাচীন ভারতে গণিতচর্চা (পর্ব-২৫১)

 প্রদীপ কুমার মজুমদার
প্রদীপ কুমার মজুমদার