প্রদীপ কুমার মজুমদার 
(গ)- মহাবীরের দ্বিতীয় পদ্ধতি:
এক ভাগশেষ এলে ভাগ করা বন্ধ কর। এখানে 6 টি ভাগফল পাওয়া যায় অর্থাৎ যুগ্মসংখ্যক ভাগফল পাওয়া যাচ্ছে।
মহাবীর t = 1 (প্রথম আর্যভটের প্রণীত মান) নিয়েছেন।
∴ y = 63 + 1530
যখন 63 দ্বারা লঘুকরণীতে পরিবর্তিত (reduced) হয় তখন
y এর লঘিষ্ট মান, y = 18
x ,, , , , ,x = 30
(ঘ) দ্বিতীয় আর্যভটের প্রণালী:
ক্ষেপ ও ভাজক থেকে G. C. M. 9. অপসারণ কর এবং পরিবর্তিত ক্ষেপ ও ভাজ্যের G. C. M 10
পরিবর্তিত (reduced) ভাজক=7
” ভাজ্য=10
” ক্ষেপ= 1
অতএব দ্বিতীয় আর্যভটের প্রণালী থেকে নিম্নলিখিত শৃঙ্খল পাওয়া যায়।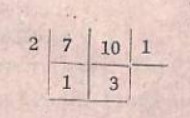 
1 -> 1 × 2 + 1 = 3
2
1
পরিবর্তিত ভাজক, ভাজ্য ও ক্ষেপসহ ভাগফল এবং গুণক 2
অতএব প্রদত্ত ভাজক, ভাজ্য এবং ক্ষেপসহ
ভাগফল x = 3× 10 = 30
গুণক y = 2 × 9 = 18
(ঙ) দ্বিতীয় ভাস্করাচার্যের প্রণালী:
(ঙ১) প্রথম আর্যভটের শৃঙ্খলে t = 0 ধরে
সর্বোচ্চ সংখ্যা থেকে x = 2430 y = 1530 পাওয়া যায় সর্ববৃহৎ নিয়ে পরিবর্তিত করলে x = 30 y = 18 পাওয়া যায়।
(ঙ২) ভাজ্য ও ক্ষেপ থেকে H. C. F 10 অপসারণ কর।
ভাজক=63, পরিবর্তিত ভাজ্য=10, পরিবর্তিত ক্ষেপ=9।
দ্বিতীয় ভাস্করাচার্যের নিয়ম অনুযায়ী
নিম্নলিখিত শৃঙ্খল পাব
0 -> 0 × 171 + 27 = 27
6 -> 6 ×27 + 9 = 171
3 -> 3 × 9 + 0 = 27
9
0
(চলবে)
