সূত্রটি খুব বেশী পরিষ্কার নয়। ফলে এই শ্লোকছটির অনুবাদ এবং ব্যাখ্যা দিতে গিয়ে দেশী বিদেশী গবেষকদের মধ্যে বিতর্ক সৃষ্টি হয়েছে
এক মাত্রার অনির্ণেয় সমীকরণ সম্পর্কে আলোচনা
এক মাত্রার অনির্ণেয় সমীকরণ প্রধানত দুইভাগে বিভক্ত।
যেমন
(১) এক মাত্রার অনির্ণেয় সমীকরণের একটি সমীকরণ
(২) এক মাত্রার অনির্ণেয় সহ সমীকরণ।
প্রথমটি আবার নিম্নলিখিত ভাগে বিভক্ত।
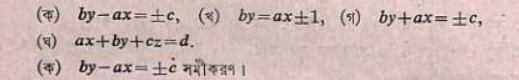
আর্যভটের পদ্ধতি: এই ধরনের সমীকরণ সম্পর্কে ভারতীয়দের মধ্যে প্রথম আর্যভটই সর্বপ্রথম ব্যাপকভাবে আলোচনা করেন। তিনি গণিতপাদের ৩২-৩৩ শ্লোকদ্বয়ে বলেছেন:
অধিকাগ্রভাগহারং ছিন্দ্যাদুনাগ্রভাগহারেণ। শেষপরস্পরভক্তং মতিগুণমগ্রান্তরে ক্ষিপ্তম্। অধউপরি গুণিতমন্ত্যযুগুণাগ্রচ্ছেদ্রভাজিতে শেষম্। অধিকাগ্রচ্ছেদগুণং দ্বিচ্ছেদাগ্রমধিকাগ্রযুতম্।
সূত্রটি খুব বেশী পরিষ্কার নয়। ফলে এই শ্লোকছটির অনুবাদ এবং ব্যাখ্যা দিতে গিয়ে দেশী বিদেশী গবেষকদের মধ্যে বিতর্ক সৃষ্টি হয়েছে। যাই হোক বর্তমানে ডঃ বিভূতিভূষণ দত্তের ব্যাখ্যাই অধিকাংশ গবেষক এবং পণ্ডিত মেনে নিয়েছেন। ডঃ দত্ত তাঁর গবেষণামূলক প্রবন্ধে যে আলোচনা করেছেন তা শুধু মনোগ্রাহীই ছিল না সঙ্গে ছিল সুদৃঢ় যুক্তির বিস্তার। তিনি এই শ্লোক দুটিকে এইভাবে ভেঙ্গেছেন:
(ক) অধিকাগ্রভাগহারং ছিন্দ্যাদৃণাগ্রভাগহারেণ,
(খ) শেষ পরস্পর ভক্তৎ
(গ) মতিগুণং অগ্রান্তরে ক্ষিপ্তম্।
(ঘ) অধউপরিগুণিতং অন্ত্যাযুক্।
(ঙ) উনাগ্রচ্ছেদভাজিতে শেষং অধিকাগ্রচ্ছেদগুণং অধিকাগ্রযুতম্।
(চ) দ্বিচ্ছেদাগ্রম,।
অর্থ হচ্ছেঃ (ক) বৃহৎ ভাগশেষের সঙ্গে সংশ্লিষ্ট ভাজককে ক্ষুদ্র ভাগশেষের সঙ্গে সংশ্লিষ্ট ভাজক দিয়ে ভাগ দাও (Divide the divisor corresponding to the greater remainder by the divisor corresponding to the smaller remainder).
(খ) এটি আবার চারটি ভাবে প্রকাশ করা যায় যেমন:
(খ১) অন্যোন্য ভাগের শেষ ভাগশেষ (The last remainder of the mutual division).
(খ২) অন্যোন্য ভাগের শেষ ভাগফল (The last quotient of the mutual division).(খত। অবশিষ্ট (এবং ক্ষুদ্র ভাগশেষের সঙ্গে সংশ্লিষ্ট ভাজক) অন্ত্যোন্তরূপে ভাগ দাও, শেষ অবশিষ্ট (The residue and the divisor corresponding to the smaller remainder) being mutually divided, the last residue ).
(খ) অবশিষ্ট (এবং ক্ষুদ্র ভাগশেষের সঙ্গে সংশ্লিষ্ট ভাজক) অন্যোন্যরূপে ভাগ দাও, শেষ ভাগ ভাগফল [The residue (and the divisor corresponding to the smaller remainder) being mutually divided, the last quotient).
(চলবে)

 প্রদীপ কুমার মজুমদার
প্রদীপ কুমার মজুমদার