আমরা by=ax+c সমীকরণটি প্রথম আর্যভটের প্রণালীতে সমাধান করে দেখাচ্ছি। অবশ্য এখানে ৫ এবং b মৌলিক সংখ্যা ধরা হয়েছে।

এখন..

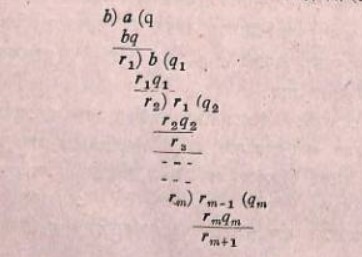
তাহলে (যখন a < b তখন আমরা পাই q = 0R₁ = a ) দেখা যাচ্ছে
a = bq +R₁

b = R₁q₁ +R₁

r m – 1 =r m-1 q m-1 +r m

r m – 1 =r m q m +r m+1

a-এর মান by = ax + c সমীকরণটিতে বসালে পাওয়া যায় by = (bq + r₁} x) + c অতএব y = qx + y₁ এখানে by₁ = r₁x + c

যেহেতু a = bq + r₁ মান বসানোর পর আমরা পাই y= qx +y 1 ……….[1] এখন b_{v} = ax + c পরিবর্তিত হয়ে দাঁড়ায় by =r 1 x+c…………..[1.1]

আবার যেহেতু b = r₁q₁ + r₂

ঠিক একইভাবে বসালে আমরা পাই x = q₁ y + x₁ তাহলে [1.1] পরিবর্তিত আকার ধারণ করে এইরূপ হয়

r₁x₁ = r₂ y₁ – c [1.2].

এইভাবে যদি এই পদ্ধতি অনুসরণ করা যায় তাহলে আমরা নিম্নলিখিত সমীকরণ সমূহ পাই।

[1] y = qx + y_{1                                            bY1 =R1 x + c                                [1-1]}

[2] x = q₁y + x₁                                       r₁x₁ = r₂y₁ – c                         [1.2]

[3] y₁  = q₂ x₁+ y₂                                  r₂ y₂  = r₃ x₁ + c                     [1.3]

[4] x₁ = q₃ y₂ + x₂                                   r₃x₂  = r₄ y₂  – c                     [1.4]

…

[25] x s – 1 =q 2s-1 y s +x s r y, n – 1 x s =r 2,n y s -c                  [1’2s]

[2s + 1] y s =q 2 x s +y s + 1 r 3, y y s+1 =r 2,s+1 x s +c        [12s+1]

এখন আমরা দুটি ক্ষেত্র পাব (১) পারস্পরিক ভাগ করার ফলে এমন এক জায়গায় পৌঁছাব যেখানে কোন অবশিষ্ট থাকবে না। (২) অথবা নির্দিষ্ট সংখ্যক ভাগফল পাবার পর আমরা আর অগ্রসর হবো না। যে কোন ক্ষেত্রই হো’ক আমরা প্রথম ভাগফলটিকে বাদ দেবো।

(১.) যখন শূন্য অবশিষ্ট থাকছে: যেহেতু ৫ এবং b পারস্পরিক মৌলিক। অতএব শেষ ভাগশেষের ঠিক পূর্বের ভাগশেষ এক হবে।

(চলবে)

প্রাচীন ভারতে গণিতচর্চা (পর্ব-৩০৭)

প্রাচীন ভারতে গণিতচর্চা (পর্ব-৩০৭)