প্রদীপ কুমার মজুমদার 
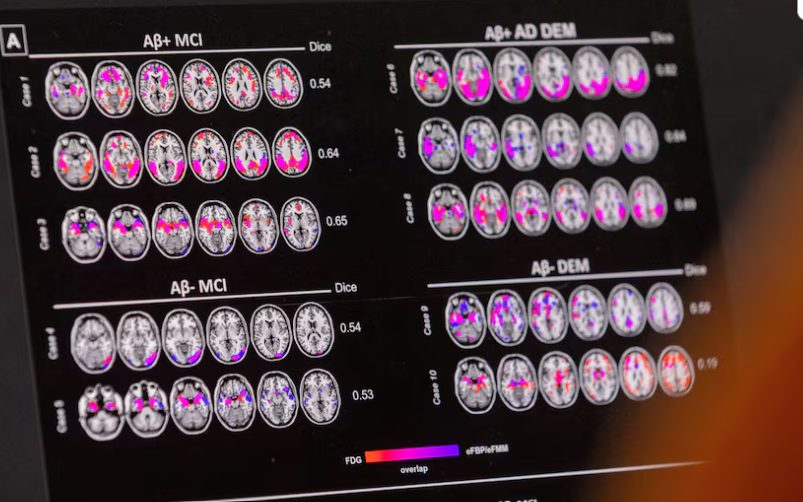
গণিতসার সংগ্রহে মহাবীর একটি উদাহরণ এবং তার সমাধান করেছেন এবং তাঁর উদাহরণ থেকে স্পষ্টই বোঝা যায়…
শ্রীধরাচার্য বলেছেন-
চতুরাহতবর্গসমৈ রূপেঃ পক্ষদ্বয়ং গুণয়েত।
অব্যক্তবর্গরূপেরুক্তৌ পক্ষৌ মূলম্
অর্থাৎ অব্যক্তের বর্গের গুণকের চতুগুণ দ্বারা উভয়পক্ষকে গুণ করা কর্তব্য।
তারপর উভয়পক্ষে অব্যক্তের গুণকের বর্গের যোগ এবং পরবর্তী পর্যায়ে উভয় পক্ষের বর্গমূল নির্ণয় কর। অর্থাৎ
ax ² + bx + c = 0 দ্বিঘাত সমীকরণটি সমাধান করতে হলে
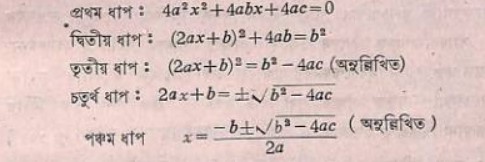
দ্বিঘাতের দুটি বীজ আছে কি নেই সে কথা শ্রীধরাচার্যের ক্ষেত্রে বলা দুষ্কর।
ত্রিশতিকায় সমান্তর প্রগতি নিয়ে আলোচনা করতে গিয়ে তিনি দ্বিঘাত সমীকরণের অজ্ঞাত রাশি বের করার সূত্র দিয়েছেন।
গণিতসার সংগ্রহে মহাবীর একটি উদাহরণ এবং তার সমাধান করেছেন এবং তাঁর উদাহরণ থেকে স্পষ্টই বোঝা যায় যে তিনি দ্বিঘাত সমীকরণের দুটি বীজ থাকে তা জানতেন। তিনি বলেছেন-
শিখিনাং ষোড়শভাগঃ স্বগুণশ্রুতে তমাকেষড়েইস্থাত,।
শেষনবাংশ স্বহতশ্চচতুরগ্রদশাপি কাতি তে স্থ্যঃ।
(চলবে)
প্রাচীন ভারতে গণিতচর্চা (পর্ব-৩৫০)
