প্রদীপ কুমার মজুমদার 
প্রত্যেকটিকে 4টি সমান অংশে বিভক্ত করে প্রথম চারটি A21 এবং Aa1 এর মাথায় বসান হোল এবং দ্বিতীয় চারটি A₁ এবং As₁ এর পাশে বসান হ’ল।
এই লম্ব সারিগুলি দেবার পর থিবো একটি উদাহরণ দিয়ে বুঝিয়েছেন কি করে ভারতীয়রা এই আসন্নমান পেয়েছিলেন। কিন্তু থিবোর পদ্ধতির চেয়ে বি. বি. দত্তের গ্রন্থে একটি সুন্দর পদ্ধতির উল্লেখ করা হয়েছে। ২ পদ্ধতি হচ্ছে-
A এবং B দুটি বর্গক্ষেত্র লওয়া হ’ল যাদের বাহুর দৈর্ঘ্য এক একক এখন Bকে সমান তিনটি A1, A2, A3 অংশে ভাগ করা হল। As কে আবার Aa1, Asi এবং Aas, সমান এই তিনটি অংশে বিভক্ত করা হোল। এবার A বর্গ ক্ষেত্রটির মাথায় Agকে এবং Asiকে বসান হল (চিত্রে Asai, A’s1 দেখান হয়েছে) ফলে একটি নূতন বর্গক্ষেত্র M গঠিত হোল। এইবার A32 এবং A33 এর প্রত্যেকটিকে 4টি সমান অংশে বিভক্ত করে প্রথম চারটি A21 এবং Aa1 এর মাথায় বসান হোল এবং দ্বিতীয় চারটি A₁ এবং As₁ এর পাশে বসান হ’ল। এবং একটি ছোট বর্গক্ষেত্র (ডানদিকের মাথার যে ক্ষুদ্র বর্গক্ষেত্রটি আছে।)
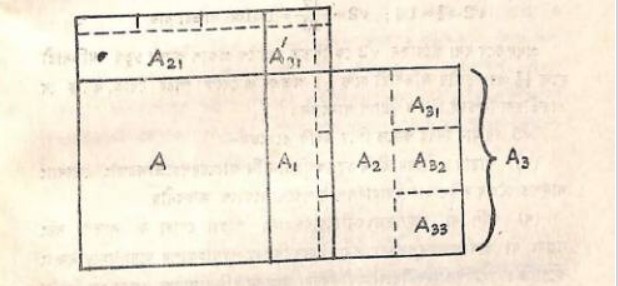
যোগ করার ফলে একটি নূতন বড় বর্গক্ষেত্র গঠিত হল যার বাহুর পরিমাপ 1 + 1/3 + 1/3.4 তাহলে আমার দেখতে পাচ্ছি নূতন বর্গক্ষেত্রটি পূর্বের দুটি বর্গ-ক্ষেত্রের যোগফল অপেক্ষা (1/3.4) ^ 3 অংশ বেশী। সুতরাং নূতন বর্গক্ষেত্রটিকে একটি ছোট বর্গক্ষেত্রে পরিণত করতে গেলে উভয় ধার থেকে সরু সরু দুটি ক্ষেত্র বাদ দেব। ধরা যাক, প্রন্থ ম। সুতরাং,
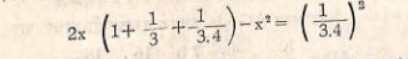
যদি x² কে অত্যন্ত ক্ষুদ্র মনে করে বাদ দেওয়া যায় তাহলে আমরা পাব
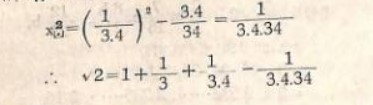
ঠিক এই পদ্ধতি ব্যবহার করে vee 3 = 1 + 2/3 + 1/3.5 – 1/(3.5 * 0.52) নির্ণয় করা হয়েছে।
“মানব শুষ সূত্রে” sqrt(2) এর মান কিছুটা পার্থক্য দেখা যায় এখানে, 40 ^ 2 + 40 ^ 2 = 56 ^ 2 4′ + 4 ^ 2 = (5 ^ (3/3)) ^ 2 এই সম্পর্ক দুটি থেকে v * 2 = 17/12 =1^ * 4166 sqrt(2) = 7/5 =1^ * 4 পাওয়া যায়।
(চলবে)
