গুরু গোবিন্দ চক্রবর্তী মনে করেন পীথাগোরাস অমূলদ রাশি সম্পর্কে জানতে পারেন বৈদেশিক প্রভাবহেতু।

শুদ্বস্থত্রে বর্গক্ষেত্রকে আয়তক্ষেত্র, আয়তক্ষেত্রকে বর্গক্ষেত্র প্রভৃতি রূপান্তর এবং আয়তক্ষেত্রের কর্ণের উপর অথবা বর্গক্ষেত্রের কর্ণের উপর অঙ্কিত ক্ষেত্রের জ্যামিতিক অঙ্কন থেকে প্রাচ্য ও পাশ্চাত্য পণ্ডিতেরা এই অনুমান করেছেন। যেমন ধরা যাক কোন আয়তক্ষেত্রের ক্ষেত্রফল A থেকে একটি বর্গক্ষেত্র যার বাহু a বাদ দিতে হবে।

সেক্ষেত্রে-

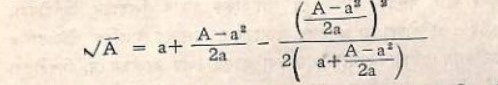
বাক্শালীর পাগুণ্ডুলিপিতে যে আধুনিক গণিতের ভাষায় রূপ দিলে দাঁড়ায়

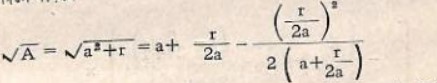
অবশ্য এই সূত্রটি গ্রাহ হবে যদি r<a রডেট বিভিন্ন শুল্বসূত্র পর্যালোচনা করে বলেছেন:

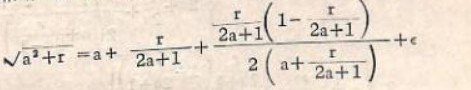
বহু ঐতিহাসিক মনে করেন ভারতীয়রা √2 প্রভৃতির অমূলদত্ব-জানতেন না। কিন্তু কিন্তু জি খিবো বলেছেন প্রাচীন ভারতীয় গণিত গ্রন্থসমূহ দেখে মনে হয় যে ভারতীয়রা √2 প্রভৃতি রাশির অমূলদত্ব জানতেন। ফন শ্রেডার তাঁর প্রবন্ধে এ মতকে সমর্থন জানিয়েছেন। বার্ক শ্রেডারকে অনুসরণ করেছেন। আর গার্বে Philosophy of ancient India গ্রন্থে, ই. ডব্লিউ হপকিনস্ Religion of India গ্রন্থে, এ. এ. ম্যাকডোনেল History of Sanskrit literature গ্রন্থে থিবোর মতকেই সমর্থন করেছেন কিন্তু অপরপক্ষে এইচ ৎসেনখেন “Theorem de Pythagore, এম. ক্যান্টর über dieälteste indische Mathematik, এইচ ফোগট Haben die alten Indian den Pythagoreisechen Lehrsatz und das Irationale gekannt ?’ প্রভৃতি প্রবন্ধ সমূহে এ মতকে নক্ষাৎ করে দিয়েছেন”।

এঁদের অনেকেই এ ব্যাপারে গ্রীকদের প্রতি ঝুঁকেছেন। যাঁরাই হউন না কেন, কেউ স্পষ্ট করে বলতে পারেন না যে গ্রীকরা কখন অমূল্য রাশি সম্পর্কে জ্ঞান আহরণ করেছিল। এটি তাদের নিজস্ব আবিষ্কার অথবা ভারতীয় বা বিদেশীদের কাছ থেকে পাওয়া কিনা তা বলা শক্ত। গুরু গোবিন্দ চক্রবর্তী মনে করেন পীথাগোরাস অমূলদ রাশি সম্পর্কে জানতে পারেন বৈদেশিক প্রভাবহেতু।

(চলবে)