প্রদীপ কুমার মজুমদার 
ভারতীয়রা স্বাধীনভাবে এবং একান্ত নিজস্ব পদ্ধতিতে রাশির অমূলদত্ব হৃদয়ঙ্গম করেছিলেন। এবং তাতে কোন বৈদিশির প্রভাব ছিল না।
অমূলদ রাশি সম্পর্কে গ্রীকরা যে জ্যামিতিক প্রমাণ দিয়েছেন মিশরীয়রা, ব্যাবিলনীয় ও ভারতীয়রা তা অন্যভাবে জানতেন। অধ্যাপক টি এরিক পীট রাইন্দ ম্যাথেমেটিক্যাল পেপিরাস সম্পর্কে আলোচনা করতে গিয়ে বলেছেন যে, মিশরীয়রা 3² + 4² = 5² এর জ্যামিতিক প্রমাণ জানতেন না। 400 গ্রীষ্টপূর্বে ডেমোক্রিটাস Harpendnataus অর্থাৎ rope Strecher সম্বন্ধে উল্লেখ করেছেন এবং এটি সমসূত্র নিরঞ্চক এর এখানে
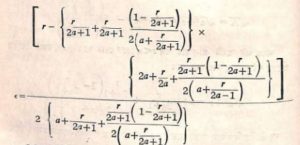
বিভিন্ন বেদী নির্মাণ করতে গিয়ে ভারতীয়রা করণী নিরসন (Rationalisation) পদ্ধতির প্রয়োগ করেছেন। বিশেষ করে “সৌত্রামণিকী বেদী” এবং “অশ্বমেধচিতি” নির্মাণ করতে গিয়ে এই পদ্ধতির ব্যবহার পরিলক্ষিত হয়। সৌত্রামণিকী বেদী সমদ্বিবাহু ট্রাপিজিয়মের মত দেখতে, এর বাহুগুলি যথাক্রমে 24/√3, 30/ √3 ও 36/√3 প্রক্রম ধরা হয়।
ঐতিহাসিকেরা বলেন 24/ √3= 8 √3 = 10 √3 এবং 36/√3 = 12 √3 প্রক্রম ভারতীয়রা জানতেন। এবং এরই সাহায্যে সমদ্বিবাহু ট্রাপিজিয়মের ক্ষেত্রফল ভারতীয়রা বের করেছেন। অর্থাৎ সমদ্বিবাহু ট্রাপিজিয়মের ক্ষেত্রফল:
36/√3× 1/2 ( 24/√3 + 30/ √3 )=324 ধরা হয়েছে।
প্রসঙ্গক্রমে বলা প্রয়োজন ভারতীয়রা বিশেষ করে শুবসূত্রকারেরা = √2 , ত্রিকরণী = √3 , =√7 তৃতীয় = √1/3 সপ্তম = √1/7 ,অষ্টাদশ করণী = √18 প্রভৃতি অর্থ করেছেন।
সমসূত্র নিরঞ্চক শব্দটি বৈদিক যুগে ব্যবহৃত হতে দেখা যায়। তাছাড়া অনেকে অনুমান করেন যে পীথাগোরাস যখন ভারতে আসেন সেই সময় হয়তো তিনি ভারতীয়দের কাছ থেকে রাশির অমূলদত্ব জেনে যান। এবং দেশে গিয়ে জ্যামিতিক পদ্ধতির সাহায্যে আলোচনা করেন। অবশ্য ভারতীয়রা পাটা-গণিতীয় অভ্যন্ত ছিল। সুতরাং সমস্ত কিছু বিগব বিশ্লেষণ করে এটুকু বলা যায় যে ভারতীয়রা স্বাধীনভাবে এবং একান্ত নিজস্ব পদ্ধতিতে রাশির অমূলদত্ব হৃদয়ঙ্গম করেছিলেন। এবং তাতে কোন বৈদিশির প্রভাব ছিল না।
(চলবে)
