শ্রেণী সম্পর্কে ভারতীয় গণিতবিদেরা আরও বেশী চিন্তা-ভাবনা করার ফলে আরও নানা ধরণের শ্রেণীর সাক্ষাৎ মিলতে থাকে।

যার মমার্থ হচ্ছে一

a + (ar ± m) +{(ar ± m)  r± m } + [{(ar ± m)  r + m} r ± m] +… +……….. +-তম পদ।

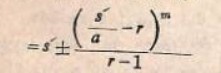
s‘ = a + ar + a r³ +………….. +n-তম পদ।

দ্বিতীয় ভাস্করাচার্য গুণোত্তর শ্রেণী সম্পর্কে আলোচনা করলেও কিছুটা অস্পষ্ট এবং প্রকৃত সূত্রের অনুপস্থিতি লক্ষ্য করা যায়। তবে তিনি কিছু উদাহরণ দিয়েছেন।
বাক্কালীর পান্ডুলিপিতেও শ্রেণীর ব্যবহার লক্ষ্য করা যায়। যেমন:

১ (ক). a₁ +  + 2a₁ + 3a₁ +………..+na₁

২(খ). a₁ + 2a₁ + 3a₂ +4a₂……+na _n-1

৩ (গ). a₁ + 2a₁ + 3( a₁ +a₂ )+4 (a₁ + a₂+a₃)+……..

এই প্রক্রিয়াকে যুতিবর্গক্রম বলা হয়েছে। (ক), (খ) ও (গ) এবং জামাত
b+(b+d)+(b+2d)+সাহায্য নিয়ে নিম্নোক্ত শ্রেণী গঠিত হয়েছে।১
s().a₁+(2ab)+30+(b+d)+44+(b+2d)+
(5). a1+(24+b)-3a+(b+d)}+{4a,+(b+2d)}+
(5). a1+(241+b)+{3(a-a₂)(+b+d)}+{4(a,+a2+as) +(b+2d)

এগুলিকে সাধারণত যুতগণিত ঋণকর্মের যুতকর্ম বলা হয়ে থাকে। এছাড়াও ভারতীয় অন্যান্য গণিতগ্রন্থে শ্রেণী সম্পর্কে আলোচনা করা হয়েছে। যাই হ’ক আমরা লক্ষ্য করলাম যে বৈদিক সাহিত্যে যুগ্ম ও অযুগ্ম সংখ্যাজাত শ্রেণীর উল্লেখ রয়েছে। তারপর শ্রেণী সম্পর্কে ভারতীয় গণিতবিদেরা আরও বেশী চিন্তা-ভাবনা করার ফলে আরও নানা ধরণের শ্রেণীর সাক্ষাৎ মিলতে থাকে। এ সম্পর্কে নবম শতাব্দীতে নেমীচন্দ্র লিখিত ত্রিলোকসারে ১৪ ধরণের শ্রেণীর কথা উল্লেখ করা হয়েছে।
যথা:

(১) সর্ব অর্থাৎ 1, 2, 3 … # স্বাভাবিক সংখ্যাদির শ্রেণী
(২) সম অর্থাৎ 2,4,6 20 সংখ্যাদির শ্রেণী
(৩) বিষম অর্থাৎ 1, 3, 5 (2pi – 1) সংখ্যাদির শ্রেণী
(৪) কৃতি অর্থাৎ 1² 28, 3² n² সংখ্যাদির শ্রেণী
(৫) অকৃতি, অবর্গ অর্থাৎ 2, 3, 5, 6 (-1) সংখ্যাদির শ্রেণী
(৬) ঘন অর্থাৎ 1ª, 2³ 3″, 48 সংখ্যাদির শ্রেণী n³
(৭) অঘন অর্থাৎ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 অর্থাৎ ঘনমূল করা যায় এমন সংখ্যা বাদ দিয়ে অন্যান্য সংখ্যা।
(৮) কৃতিমাতৃকা অর্থাৎ 1, 2 2. সংখ্যাদির শ্রেণী √n
(১) অকৃতিমাতৃকা অর্থাৎ √n+ 1 সংখ্যাদির শ্রেণী √n + 2
(১০) ঘনমাতৃক
(১১) অঘনমাতৃক অর্থাৎ অঘ+1, অঘ+2, সংখ্যাদির শ্রেণী
(১২) দ্বিরূপবর্গ অর্থাৎ 2 ^ z 2 ^ * 2 ^ n 2 ^ 16 2 ^ 32 সংখ্যাদির শ্রেণী
(১৩) দ্বিরূপঘন অর্থাৎ 2 ^ 3 (2 ^ 3) ^ 9 (2 ^ 3) ^ 4 (2), (2) সংখ্যাদির শ্রেণী
(১৪) দ্বিরূপঘন ঘন অর্থাৎ (2 ^ 3) ^ 2 = 512 ((2 ^ 8) ^ 8) ^ 8 = 262144 সংখ্যাদির শ্রেণী

(চলবে)

প্রাচীন ভারতে গণিতচর্চা (পর্ব-২৪৮)

প্রাচীন ভারতে গণিতচর্চা (পর্ব-২৪৮)