প্রদীপ কুমার মজুমদার 
কোন সংখ্যাকে তিন দিয়ে গুণ করে এক যোগ করলে বর্গ রাশি হবে; আবার পাঁচ দিয়ে গুণ করে এক যোগ করলে একটি বর্গ রাশি হবে?
ব্রহ্মগুপ্ত ব্রাহ্মস্ফুট সিদ্ধান্তের অষ্টাদশ অধ্যায়ের ৭৪-তম শ্লোকে বলেছেন-
যাভ্যাং কৃতিরধিকোনস্তদন্তরং হৃতযুতোনমিষ্টেন।
তদ্দলকৃতির ধিকোনাহধিকয়োরধিকোনয়ো রাশিঃ।
বঙ্গানুবাদ না দিলেও স্পষ্টই বোঝায় যে এখানে ব্রহ্মগুপ্ত x± a = u ², x ± b = v ²
সমীকরণদ্বয়ের সমাধানে বলেছেন:
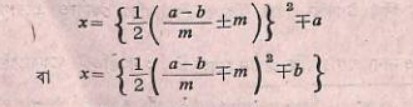
এখানে যে কোন পূর্ণসংখ্যা
দ্বিতীয় ভাস্করাচার্য অবশ্য α x + c = u ² ax + d = v ² সমীকরণদ্বয়ের সমাধানের সূত্র দিয়েছেন। তিনি বলেছেন-
“যত্রাব্যক্তৎ সরূপং হি তত্র তন্মানমানয়েত,। সরূপক্ষান্তবর্ণ কৃত্বা কৃত্যাদিনা সমম্। রাশিং তেন সমুত খাপ্য কুর্যাডুয়োহপরাং ক্রিয়াম্। সরূপেনান্যবর্ণেন কৃত্বা পূর্বপদং সমম্। ”
অনুবাদ না উল্লেখ করলেও স্পষ্টই বোঝা যাচ্ছে 4x – c = u ² x + d = v ² ধরণের সমীকরণ গুলির সমাধানের সূত্র বলেছেন। তিনি এই সঙ্গে একটি উদাহরণ দিয়েছেন।
“যন্ত্রিপঞ্চগুণো রাশিঃ পৃথক সৈকঃ কৃতির্ভবেত্।
বদতং বীজমধ্যেহসি, মধ্যমাহরণে পটুঃ
অর্থাৎ কোন সংখ্যাকে তিন দিয়ে গুণ করে এক যোগ করলে বর্গ রাশি হবে; আবার পাঁচ দিয়ে গুণ করে এক যোগ করলে একটি বর্গ রাশি হবে?
আধুনিক বীজগণিতের ভাষায় লিখলে দাড়ায়
0x + 1 = u ²
5x + 1 = v ²
এটির সমাধানও দ্বিতীয় ভাস্করাচার্য বের করেছেন। তিনি x = 16 1008 প্রভৃতি বলেছেন।
(চলবে)
প্রাচীন ভারতে গণিতচর্চা (পর্ব-৩৪৬)
