প্রদীপ কুমার মজুমদার 
অর্থাৎ,আধুনিক গণিতের ভাষায় বলতে গেলে
চতুর্বেদাচার্য এ সম্পর্কে উদাহরণে বলেছেন: সত্রিভাগং তথা সার্ধং রূপং ষড়ভাগ সংযুক্তম্। একীকৃতং ভবেক্তিং স্বং রূপত্রসমন্বিতম্ ।
ন্যাস 
যথোক্তরণেন জাতৌ রাশিঃ।৭।
অর্থাৎ এটির মর্মার্থ হচ্ছে-
‘রূপত্রয় সমন্বিতং’ এটির তাৎপর্য বলা হবে ৪+৩-৭- যোগফল= রাশি।
দ্বিতীয় ভাস্করাচার্য বলেছেন:
“যোগোহন্তরং তুল্যহরাংশকানাং কল্প্যুহরোরূপমহাররাশেঃ”।
অর্থাৎ ভগ্নাংশে যোগ অথবা বিয়োগ সমান হর গ্রহণ করতে হয়। যার ভাগফল নেই সেরূপ রাশির এক বলিয়া হর কল্পনা করতে হয়। একটি সুন্দর উদাহরণ এই প্রসঙ্গে
দ্বিতীয় ভাস্করাচার্য উল্লেখ করেছেন-
“পক্ষাংশপাদ ত্রিলবান্ধ যষ্ঠানেকী তান্ ক্রহি সথে মমৈতান্ এভিশ ভাগৈরণ বন্দিতানাং কিং স্বাৎ ত্রয়াণং কথয়ান্ড শেষম্।
ন্যাস 
ঐক্যে জাতম্ 
অথৈতৈবিবর্জিতানাং এয়াণাং শেষম্ 
বর্ণনা-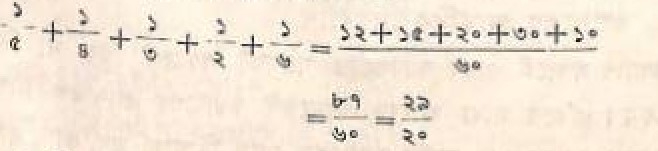 
তিন থেকে বাদ দিলে শেষ থাকবে 
(চলবে)
