প্রদীপ কুমার মজুমদার 
অবধেশ নারায়ণ সিং এ সম্পর্কে একটি সুন্দর উদাহরণ তুলে ধরে দুই পদ্ধতির সামঞ্চস্ত প্রমাণ করেছেন। তাঁর উদাহরণটি এখানে তুলে ধরলাম-
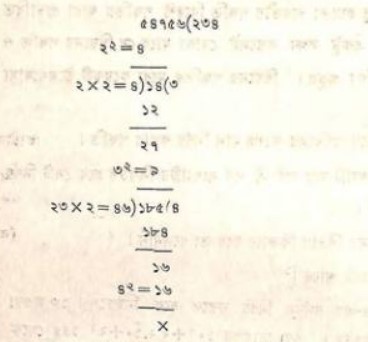
অতএব আর্যভটের পদ্ধতির সঙ্গে কাটানিওর পদ্ধতির মিল রয়েছে। যাই হোক বর্গমূল সম্পর্কে অন্যান্য ভারতীয় গণিতবিদরা কে কি বলেছেন দেখা যাক।
ত্রিশতিকায় শ্রীধরাচার্য বলেছেন-
“বিষমাত, পদতস্ত্যক্ত। বর্গং স্থানচ্যুতেন মূলেন
দ্বিগুণেন ভজেচ্ছেযং লব্ধং বিনিবেশয়েত, পড়ুক্তাম্।
তন্বর্গং সংশোধ্য দ্বিগুণী কুর্বীত পূর্ব লব্ধং যত,
উত,সার্থ ততো বিভজেচ্ছেষং দ্বিগুণীকৃতং দলয়েত,। ১২/১৩।”
গণিতসার সংগ্রহে মহাবীর বলেছেন-
“অন্ত্যোজাদপহৃতকৃতি মূলেন দ্বিগুণিতেন যুগ্মাদ্ধতৌ।
লঙ্কৃতিন্ত্যাজ্যোঁজে দ্বিগুণপদলং বর্গমূলফলম্॥”
ঘনমূল
বর্গমূলের মত ঘনমূলের সম্পর্কে আলোচনা ভারতীয় গণিতশাস্ত্রে প্রচুর দেখতে পাওয়া যায়। তবে এ সম্পর্কে পদ্ধতিগত ভাবে প্রথম আলোচনা করেন প্রথম আর্যভট। এরপর শ্রীধরাচার্য, দ্বিতীয় আর্যভট, ব্রহ্মগুপ্ত, ভাস্করাচার্য প্রমুখেরা ব্যাপক আলোচনা করেছেন। দ্বিতীয় ভাস্করাচার্য লীলাবতী গ্রন্থে বলেছেন-
“আ্যং ঘনস্থান যথাঘনে যে পুনস্তখান্ত্যদ্যনতোবিশোধ্যম্। ঘনং পৃথকস্থৎ পদমস্তা কৃত্যা ত্রিগ্ন্যা তদাখ্যং বিভজেৎ ফলন্ত। পঙক্তপংন্যদেৎ তৎকৃতিমন্ত্যনিম্নীং ত্রিগ্নীং ত্যজেৎ তৎ প্রথমাৎ ফলক্ষ্য। তদাখ্যাদ্যনমূলমেবং পঙক্তির্ভবেদেব মতঃ পুনশ্চ।”
(চলবে)
