প্রদীপ কুমার মজুমদার 
বর্গ লও তৎপর পদসমষ্টির যোগফলের সঙ্গে আটগুণ সাধারণ অন্তর গুণ করে যোগ কর।
দ্বিতীয় ভাস্করাচার্য বলেছেন:
যথোত্তরচয়েহস্ত্যাদিধনজ্ঞানায় করণসূত্রং বৃত্তম্। ব্যৈকপদয়চয়ো মুখযুক্ স্যাদন্ত্যধনং মুখধুদলিতং তত। মধ্যধনং পদসঙ্কুণিতং তত, সর্বধনং গণিতজ্ঞ তছজম্।
এই প্রসঙ্গে দ্বিতীয় ভাস্করাচার্য একটি সুন্দর উদাহরণ দিয়েছেন। তিনি বলেছেন:
আদ্যে দিনে দ্রম্মচতুষ্টয়ং যো দত্তা দ্বিজেভ্যোহহুদিনং প্রবৃত্তঃ।
দাতুং সখে পঞ্চয়েন পক্ষে দ্রম্মা বদ দ্রাকাতি তেন দত্তা।
অর্থাৎ যদি কোন লোক কোন ব্রাহ্মণকে প্রথমদিন চার দ্রম্ম এবং প্রত্যেকদিন পাঁচটি করে দ্রম্ম বেশী দিতে থাকে তাহলে একপক্ষ দিনকালে ঐ লোক কত দ্রম্ম দান করেছিল?
এখানে প্রথমপদ 4, সাধারণ অন্তর5, পদসংখ্যা=n
∴ দ্রন্ম সংখ্যা=15/2 {(2.4+(15-1)5}
=15/2 {8+70}
= 15×78 /2= 585
পদসংখ্যা নির্ণয় করার পদ্ধতি ব্রহ্মগুপ্ত ব্রাহ্মস্ফুট সিদ্ধান্তে উল্লেখ করেছেন। তিনি বলেছেন:
উত্তরহীন দ্বিগুণাদিশেষবর্গং ধনোত্তরাইবধে।
প্রক্ষিপ্য পদং শেযোণং দ্বিগুণোত্তরহৃতং গচ্ছঃ ।
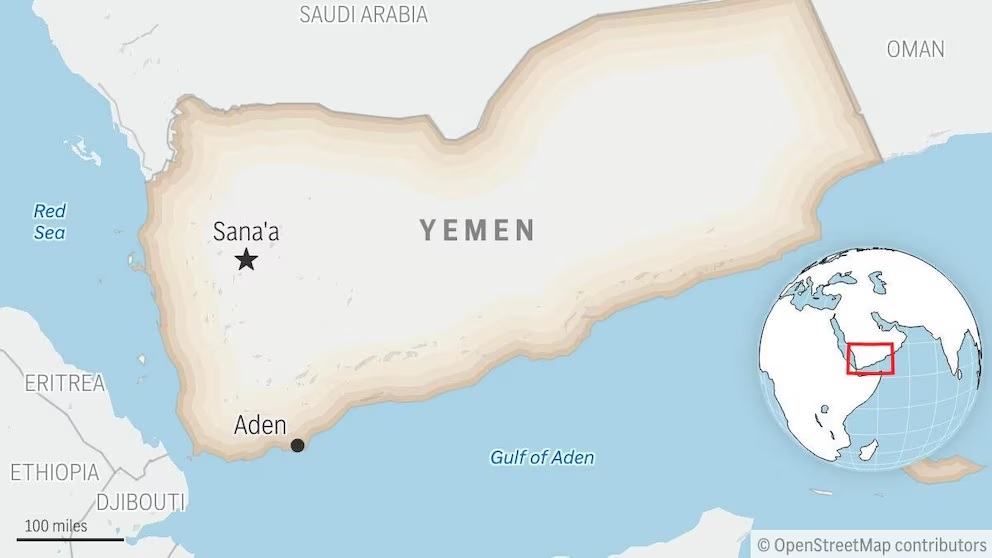
অর্থাৎ প্রথম পদের দ্বিগুণের সঙ্গে সাধারণ অন্তর বিয়োগ করে যে শেষ থাকে তার বর্গ লও তৎপর পদসমষ্টির যোগফলের সঙ্গে আটগুণ সাধারণ অন্তর গুণ করে যোগ কর। তারপর এদের মূল লও। এই মূল থেকে শেষ বিয়োগ দাও সর্বশেষে এই বিয়োগফলকে সাধারণ অন্তরের দুগুণ দিয়ে ভাগ দাও।
(চলবে)
প্রাচীন ভারতে গণিতচর্চা (পর্ব-২৪৪)
