প্রদীপ কুমার মজুমদার 
সাধারণ অন্তর এবং পদসংখ্যা জানা থাকলে শেষপদ কত সংখ্যা, মধ্যপদ কত সংখ্যা এবং যে কোন সংখ্যক পদের সমষ্টি নির্ণয় করা যেতে পারে।
আর্যভট অবশ্য 1³ +2³+…+ 10³ = (1/2.10.11)² বলেছেন, তবে ইটালীর বিখ্যাত গণিতবিদ ফিবোনাচ্চি একাদশ শতাব্দীতে এ সম্পর্কে একটি সর্বজনগ্রাহ্য সূত্র দেন। এই সূত্রটি হচ্ছে,
1³ +2³+⋅⋅⋅⋅⋅+ n³ = {1/2 n(n + 1)}² মহাবীর গণিতসার সংগ্রহের যষ্ঠ অধ্যায়ে যা বলেছেন তার মমার্থ হচ্ছে
a² + (a + b)² + (a + 2b)² +…..+n- তম পদ
এবং a³ + (a + b)³ + (a + 2b)³ +⋅⋅⋅⋅⋅⋅⋅+n- তম পদ পর্যন্ত
= s² b + sa(a – b) যদি a > b হয়
অথবা, s² b – sa(a – b) যদি a < b হয়
এখানে s= a + (a + b) + (a + 2b) +⋅⋅⋅⋅⋅+n তম পদ পর্যন্ত
প্রথম আর্যভট, মহাবীর, প্রমুখেরা সমান্তর শ্রেণী সম্পর্কে যা উল্লেখ করেছেন তার চেয়ে অনেক সুশৃঙ্খলভাবে ব্রহ্মগুপ্ত এবং দ্বিতীয় ভাস্করাচার্য আলোচনা করেছেন। a < b
ব্রহ্মগুপ্ত ব্রাহ্মস্ফুট সিদ্ধান্তের গণিতাধ্যায়ের ১৭ নং সূত্রে বলেছেন “পদমেকহীনমুত্তরগুণিতং সংযুক্তমাদিনা হস্ত্যধনম্। আদিযুতান্ত্যধনার্ধং মধ্যধনং পদগুণনং গণিতম্।
অর্থাৎ প্রথমপদ, সাধারণ অন্তর এবং পদসংখ্যা জানা থাকলে শেষপদ কত সংখ্যা, মধ্যপদ কত সংখ্যা এবং যে কোন সংখ্যক পদের সমষ্টি নির্ণয় করা যেতে পারে। পদসংখ্যা থেকে এক বিয়োগ করে ঐ বিয়োগফলকে সাধারণ অন্তর দিয়ে গুণ করে তারপর প্রথম পদ যোগ করলে শেষ পদ পাওয়া যাবে। এই শেষপদের সঙ্গে প্রথম পদ আবার যোগ দিয়ে তারপর দুই দিয়ে ভাগ দিলে মধ্যপদ পাওয়া যাবে। এই মধ্যপদকে পদ সংখ্যা দিয়ে গুণ করলে সমগ্র পদের সমষ্টি পাওয়া যাবে।
অর্থাৎ আধুনিক গণিতের ভাষায় বলতে গেলে
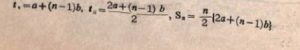
এখানে -তম পদ, এ প্রথম পদ, ৮ সাধারণ অন্তর, মধ্যম পদ। Sসংখ্যক পদের সমষ্টি।
দ্বিতীয় ভাস্করাচার্য বলেছেন:
যথোত্তরচয়েহস্ত্যাদিধনজ্ঞানায় করণসূত্রং বৃত্তম্। ব্যৈকপদয়চয়ো মুখযুক্ আাদন্ত্যধনং মুখযুগদলিতং তত। মধ্যধনং পদসঙ্কুণিতং তত, সর্বধনং গণিতজ্ঞ তছজম্।
এই প্রসঙ্গে দ্বিতীয় ভাস্করাচার্য একটি সুন্দর উদাহরণ দিয়েছেন। তিনি বলেছেন:
আদ্যে দিনে প্রশ্নচতুষ্টয়ং যো দত্তা দ্বিজেভ্যোহহুদিনং প্রবৃত্তঃ।
সাদাতুং সথে পঞ্চয়েন পক্ষে দ্রম্মা বদ দ্রাকাতি তেন দত্তা।
অর্থাৎ যদি কোন লোক কোন ব্রাহ্মণকে প্রথমদিন চার প্রশ্ন এবং প্রত্যেকদিন পাঁচটি করে ব্রহ্ম বেশী দিতে থাকে তাহলে একপক্ষ দিনকালে ঐ লোক কত প্রশ্ন দান করেছিল?
(চলবে)
প্রাচীন ভারতে গণিতচর্চা (পর্ব-২৪৩)
