প্রদীপ কুমার মজুমদার 
x এবং y অজ্ঞাতরাশিদ্বয় হলে এদের পার্থক্য এবং গুণফল দেওয়া আছে। তাহলে উপযুক্ত শ্লোকটিকে আধুনিক গণিতের ভাষায় লিখলে দাঁড়ায়…
দ্বিতীয় আর্যভটও পূর্বসূরীদের মত দ্বিঘাত সমীকরণ নিয়ে আলোচনা করেছেন।
ভারতীয় গণিতশাস্ত্র নিয়ে ব্যাপক আলোচনা করলে দেখা যাবে প্রথম আর্যভট, ব্রহ্মগুপ্ত, শ্রীধরাচার্য, শ্রীপতি, দ্বিতীয় ভাস্করাচার্য প্রমুখেরা দ্বিঘাত সহ সমীকরণ (Simulteneous quadratic equation) সম্পর্কে বেশ ভালভাবেই জানতেন। অর্থাৎ তাঁরা নিয়ে বর্ণিত সমীকরণগুলির সমাধান জানতেন।
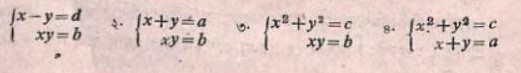
(১) প্রথম সমীকরণটির সমাধান কল্পে প্রথম আর্যভট (৪১৯ খ্রীঃ) বলেছেন
দ্বিকৃতিগুণাত, সংবর্গাদ দ্ব্যয়স্তরবর্গেণ সংযুতান্ম, লম্।
অন্তরযুক্তং হীনং তদ্ গুণকারদ্বয়ং দলিতম্।
অর্থাৎ মর্মার্থ হচ্ছে-দুটি অজ্ঞাত রাশির গুণফলকে চার দিয়ে গুণ করে ঐ গুণফলের সঙ্গে অজ্ঞাত রাশিদ্বয়ের পার্থক্যের বর্গ যোগ কর। তারপর মূল গ্রহণ কর এবং আবার অজ্ঞাতরাশিদ্বয়ের পার্থক্য যোগ বা বিয়োগ কর। এরপর সমস্ত ফলের অর্ধেক নিলে অজ্ঞাত সংখ্যা দুটি পাওয়া যাবে।
একটু ব্যাখ্যা করা প্রয়োজন। এখানে x – y = d এবং xy = b সমীকরণ দেওয়া আছে। অর্থাৎ x এবং y অজ্ঞাতরাশিদ্বয় হলে এদের পার্থক্য এবং গুণফল দেওয়া আছে। তাহলে উপযুক্ত শ্লোকটিকে আধুনিক গণিতের ভাষায় লিখলে দাঁড়ায়:
এই প্রসঙ্গে ব্রহ্মগুপ্ত বলেছেনঃ
“শেশবধাদ দ্বিকৃতিগুণাত, শেষান্তরবর্গ সংযুতান্ন, লম্।
শেষান্তরোনযুক্তং দলিতং শেষে পৃথগভীষ্ঠে
এই ধরণের সমীকরণ নিয়ে ব্রহ্মগুপ্তের পরবর্তীকালে কয়েকজন ভারতীয় গণিতবিদ আলোচনা করেছেন।
(২) দ্বিতীয় সমীকরণগুলির সমাধান কল্পে মহাবীর বলেছেন-
“রজ্জর্ধবর্গরাশেগণিতং চতুরাহতং বিশোধ্যাথ।
মূলং হি রজ্জর্ধে সংক্রমনে সতি ভুজাকোটি
(চলবে)
