প্রদীপ কুমার মজুমদার 
অনেক পণ্ডিত মনে করেন একহাজার গ্রীষ্টপূর্বাব্দেচীনে বীজগণিতের চর্চা ছিল।
ইউফ্রেতিস ও তাইগ্রিস নদীর মধ্যবর্তী অর্ধচন্দ্রাকার স্থলভাগের অধিবাসী ব্যাবিলনীয়রা বীজগণিতের প্রথম যুগে বীজগণিত সম্পর্কে কিছু আলোচনা করেছেন। নিনেভ, আসুর, নিপ্লব প্রভৃতি স্থান খনন করে যে সব মাটির চাকতি পাওয়া গিয়েছে, তাতেই দেখা গিয়েছে এই সব নিদর্শন। দৃষ্টান্তস্বরূপ মাটির চাকতি থেকে একটি উদাহরণ তুলে ধরছি।
আমি একটি পাথর দেখলাম কিন্তু ওজন করলাম না। অতঃপর আমি ১/৭ অংশ বিয়োগ করি, (এবং) ১৬ অংশ বিয়োগ করি। আমি ওজন করলাম (ইহাকে), ১ মা-ন, পাথরটির মূল ওজন কত ?
উত্তর: “পাথরটির মূল ওজন ১ মা-ন ১২ গিন এবং ২২ সে।” আধুনিক বীজগণিতের ভাষায় লিখলে দাঁড়ায়-
সমাধান-
x = 1 মা-ন+91 + 2 1/2 G = 1, 9 ; 30,50 গিন
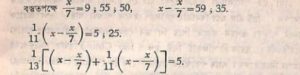
এছাড়াও পণ্ডিতেরা মাটির চাকতি পড়ে মত দিয়েছেন যে, ব্যাবিলনবাসীরা বীজগণিতের সাহায্যে এক ঘাত, দ্বিঘাত ও সহ সমীকরণের সমাধান করতে পারতেন।
চীনদেশে ঠিক কবে থেকে বীজগণিত চর্চা শুরু হয়েছিল তা বলা কঠিন।
অনেক পণ্ডিত মনে করেন একহাজার গ্রীষ্টপূর্বাব্দেচীনে বীজগণিতের চর্চা ছিল। য়োশিও মিকামী প্রমুখ গণিত ঐতিহাসিকেরা বলেন, চ্যাঙ্গ ৎসাহ্ত্র লিখিত কিউ চ্যাঙ্গ সুয়ান সু গ্রন্থে বীজগণিতের কিছু কিছু উদাহরণ দেখতে পাওয়া যায়। দৃষ্টান্তস্বরূপ তাঁরা এই গ্রন্থের কোন এক স্থান থেকে উদ্ধৃতি দিয়ে বলেছেন যে,এই দুটি সমীকরণের সমাধান এই গ্রন্থে দেখতে পাওয়া যায় এবং এই পদ্ধতিকে চি চু (chih chhu) বলা হয়।
(চলবে)
প্রাচীন ভারতে গণিতচর্চা (পর্ব-২৬২)
