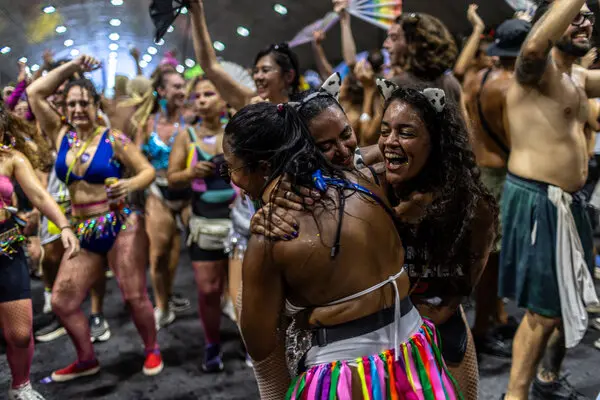দ্বিতীয় ভাস্করাচার্যের গ্রন্থাদির মধ্যে এই পদ্ধতির সীমিত প্রয়োগ দেখা যায়।

দ্বিতীয় ভাস্করাচার্য প্রায় একই কথা বলেছেন এবং সঙ্গে সঙ্গে উদাহরণ দিয়ে বুঝিয়ে দিয়েছেন। তিনি বলেছেন-

“একস্য রূপত্রিশতী ষড়শা অশ্বা দশা্যন্ত তু তুল্যমৌল্যাঃ।

ঋণং তথা রূপশতঞ্চ তস্য তৌ তুল্যবিত্তৌ চ কিমশ্বমৌল্যম্।”

অর্থাৎ প্রথম ব্যক্তির কাছে ৩০০ মুদ্রা ও ৬টি ঘোড়া আছে এবং দ্বিতীয় ব্যক্তির কাছে ১০টি ঘোড়া এবং ১০০ মুদ্রা ঋণ আছে। ঘোড়ার মূল্য কত?

আধুনিক গণিতে রূপ দিলে দাঁড়ায়, 6x+300=10x-100 উপযুরোক্ত দুইটি পদ্ধতি ছাড়াও ভারতবর্ষে আরও একটি পদ্ধতি চালু ছিল। সেই পদ্ধতির নাম Rule of false positions এবং এই পদ্ধতি বাকশালীর পাণ্ডুলিপিতে দেখা যায়।

অবশ্ব পরবর্তীকালে অধিকাংশ ভারতীয় গ্রন্থে এই পদ্ধতিটি অনুপস্থিত। তবে শ্রীধরাচার্য, মহাবীর এবং দ্বিতীয় ভাস্করাচার্যের গ্রন্থাদির মধ্যে এই পদ্ধতির সীমিত প্রয়োগ দেখা যায়।

(খ) দুটি অজ্ঞাতরাশি বিশিষ্ট একমাত্রার সরল সমীকরণ নিয়ে ব্রহ্মগুপ্ত, শ্রীপতি, শ্রীধরাচার্য, দ্বিতীয় ভাস্করাচার্য প্রমুখ ভারতীয় গণিতবিদেরা আলোচনা করেছেন।

এদের মধ্যে কেউ সূত্র দিয়েছেন, কেউবা শুধুমাত্র উদাহরণ দিয়েছেন, আবার কেউ উদাহরণ সহ সূত্র দিয়েছেন। ব্রহ্মগুপ্ত এই পদ্ধতিকে সংক্রমণ বলেছেন এবং এর সংজ্ঞা অত্যন্ত পরিষ্কারভাবে দিয়েছেন। তিনি বলেছেন:

যোগোহন্তর যুতহীনে। দ্বিহৃতঃ সংক্রমস্তরবিভক্তং বা”

অর্থাৎ দুটি রাশির যোগের সঙ্গে দুটি রাশির অন্তর যোগ এবং বিয়োগ করে দুই দিয়ে ভাগ দিলে রাশি দুটি পাওয়া যাবে। এবং এটিকে সংক্রমণ বলে।

অর্থাৎ গণিতের ভাষায় বললে দাঁড়ায়,

শ্রীপতি এই প্রসঙ্গে বলেছেন:

“যোগোহন্তরেণোনযুতো দ্বিভক্তঃ কর্মোদিতং সংক্রমণাখ্যমেতন। ”

অর্থাৎ দুইটি রাশির যোগের সহিত দুইটি রাশির অন্তরকে উৎ (বিয়োগ) যুক্ত করিয়া দুই দ্বারা ভাগ করিলে রাশিদ্বয় পাওয়া যাইবে।

মহাবীরাচার্য এ সম্পর্কে উদাহরণ দিয়েছেন যা থেকে আমরা আধুনিক বীজগণিতের ভাষায় বলতে পারি,

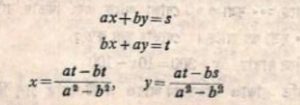
(চলবে)