অনির্ণেয় সমীকরণের সঙ্গে জড়িত সব গাণিতিক উদাহরণগুলিকে দুটি শাখায় বিভক্ত করেছেন।

এক মাত্রার অনির্ণেয় সমীকরণের বিভাগ

একমাত্রার অনির্ণেয় সমীকরণ তিনটি ভাগে বিভক্ত এবং এগুলি হচ্ছে: (ক) কোন সংখ্যা (N) কে ছটি প্রদত্ত রাশি ৫ এবং b দ্বারা ভাগ করলে দুইটি প্রদত অবশেষ (Remainder) R₁ এবং R₂ পাওয়া যাবে। অর্থাৎ এ থেকে আমরা পাই

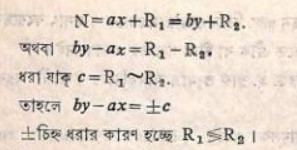
(খ) এমন কোন একটি রাশি (x) নির্ণয় করতে হবে যাকে অন্য একটি প্রদত্ত রাশি দিয়ে গুণ করে ঐ গুণফলের সঙ্গে অন্য একটি প্রদত্ত রাশি (৮) যোগ বা বিয়োগ করার পর তৃতীয় কোন রাশি (৫) দিয়ে ভাগ করলে কোন অবশিষ্টাংশ থাকবে না। অর্থাৎ

(গ) তৃতীয় ধরণের অনির্ণেয় সমীকরণ হচ্ছে

by+ax=±c.

প্রথম ভাস্করাচার্যই হচ্ছেন প্রথম ভারতীয় গণিতবিদ যিনি একমাত্রার অনির্ণেয় সমীকরণের সঙ্গে জড়িত সব গাণিতিক উদাহরণগুলিকে দুটি শাখায় বিভক্ত করেছেন। এই দুটি শাখা হচ্ছে (ক) সাগ্র কুটাকার (খ) নিরগ্র কুট্রাকার। প্রথম ভাস্করাচার্য এই দুই শাখাকে উদাহরণের সাহায্যে ব্যাখ্যা করেছেন তিনি সাগ্র কুটাকার (Residual Pulveriser) সম্পর্কে নিম্নোক্ত উদাহরণ দিয়েছেন:

পঞ্চভিরেকং রূপং দ্বে রূপে চৈব সপ্তভাগেন।
অবশিক্ষতে তু রাশিবিগণ্যতাং তত্র কা সংখ্যা।

এটির মর্মার্থ হচ্ছে-এমন একটি রাশি নির্ণয় কর যাকে ৫ দিয়ে ভাগ করলে ১ অবশিষ্ট থাকে; এবং ৭ দিয়ে ভাগ করলে ২ অবশিষ্ট থাকে।

(চলবে)