প্রদীপ কুমার মজুমদার 
বহু পাশ্চাত্ত্য গণিত ঐতিহাসিক দ্বিতীয় ভাস্করাচার্য বা প্রথম আর্যভটের প্রণালীকে গ্রীক প্রণালী বলে অভিহিত করেন।
উদাহরণের প্রকার চা৯৮১/১৯৬/৮৮২০৯/১০০১০০০২৫ এইভাবে ক্রমে ক্রমে বর্গ পাওয়া যাইল-২/৩/১/১৪/২৯৭/১০০০৫।
ভাস্করাচার্যের প্রণালীতে ১০০১০০০২৫-এর বর্গমূল করা যাক।
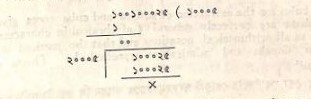
বর্গমূল সম্পর্কে প্রথম আর্যভট আর্যভটীয়ের গণিতপাদের চতুর্থ শ্লোকে বলেছেন:
“ভাগং হরেদবর্গান্নিত্যং দ্বিগুণেন বর্গমূলেন
বর্গাদ্বর্গৈ শুদ্ধে লব্ধং স্থানান্তরে মূলম্।”
ব্যাখ্যা নিষ্প্রয়োজন।
অবধেশ নারায়ণ সিং এ প্রসঙ্গে একটি সুন্দর উদাহরণ তুলে ধরে ব্যাপারটিকে পরিষ্কার করে দিয়েছেন। তিনি ৫৪৭৫৬-এর বর্গমূল প্রথম আর্যভটের নিয়মে করেছেন। এখানে সেটি তুলে ধরা হল।
বহু পাশ্চাত্ত্য গণিত ঐতিহাসিক দ্বিতীয় ভাস্করাচার্য বা প্রথম আর্যভটের প্রণালীকে গ্রীক প্রণালী বলে অভিহিত করেন। যাঁরা এ মতের সমর্থক তাঁদের মধ্যে অধ্যাপক ডি. ই. স্মীথ এবং জি. আর. ক্যে অন্যতম। স্মীথ তাঁর হিস্ট্রী অব ম্যাথেমেটিকস, দ্বিতীয় খণ্ডের ১৪৪-১৪৮ পৃষ্ঠায় বলেছেন যে, মূলাকর্ষণের যে পদ্ধতিটি দ্বিতীয় ভাস্করাচার্য আলোচনা করেছেন সেটি আলেকজান্দ্রীয়বাসী থিয়ন প্রদত্ত। এটি সম্ভবতঃ আরবদের মাধ্যমে ভারতীয়রা জেনেছে। যতদূর মনে হয় স্মীথ জি. আর. ক্যের কোন একটি প্রবন্ধ পাঠ করে এই মন্তব্যটি করেছেন। ক্যে’র প্রবন্ধটির উল্লেখযোগ্য অংশটি যেটি ‘স্মীথ হয়তো দেখে উপরোক্ত মন্তব্য করেছেন সেটি হচ্ছে:
“The rules for the extraction of square and cube roots given by Aryabhata are perfectly general (algebraical in character) and apply to all arithmetical notations and that the method was known to Greeks and admirably expressed by Theon of Alexandria.”
মনে হয় ক্যে আর্যভটের শ্লোকটি হৃদয়ঙ্গম করতে পারেন নি এবং ইংরাজীতে যে তর্জমা করেছিলেন তা ভ্রমে পূর্ণ ছিল।
(চলবে)
প্রাচীন ভারতে গণিতচর্চা (পর্ব-২২০)
