প্রদীপ কুমার মজুমদার 
যে সূত্রসমূহ শুষস্থত্রে দেখা যায় তার উপর ভিত্তি করে প্রাচ্য ও পাশ্চাত্য পণ্ডিতেরা একটি নিয়ম খাড়া করেছেন।
প্রসঙ্গক্রমে বলা প্রয়োজন √2 কে বিতত ভগ্নাংশে প্রকাশ করলে চতুর্থ অভিসারী হচ্ছে এবং তৃতীয় অভিসারী হচ্ছে। অতএব এ থেকে স্পষ্টই বোঝা যাচ্ছে যে ভারতীয়রা নিশ্চয়ই বিতত ভগ্নাংশ জানতেন।
√5 এর মান নির্ণয় করতে গিয়ে মহর্ষি বলেছেন-
(ক) আয়াম তৃতীয়েন ত্রীনি চতুরপ্রণ্যনুচীনানি কারয়েদপরস্থ্যোত্তরগ্যাং শ্রোণ্যাং গার্হপত্যস্তস্তৈব দক্ষিণেহংসেহগাহার্য পপচন পূর্বসোত্তরেহংশ আহবনীয়
(খ) অপি বা গার্হপত্যাহবনীয়যোরন্তরালং পংচধা যোঢ়া বা সংভুজ্য ষষ্ঠৎ সপ্তমং বা ভাগভগন্তকম্পসমস্য সমং ত্রৈধং বিভজ্য পূর্বস্মাহন্ত্যপদ দ্বয়োভাগয়োলক্ষণং করোতি। গার্হপত্যাহবনীয়যোরম্ভৌ নিয়ম্য লক্ষণেন দক্ষিণাপায়ম্য লক্ষণে শম্ভু নিহস্তি
তদক্ষিণাগ্নেরায়তনং ভবতি।
(গ) অপি বা প্রমাণং পচমেন বর্ধয়েতসর্ব পংচধা সংভূজ্যা পরস্মাদন্ত্যাদ দ্বয়ো-ভাগযোর্লক্ষণং করোতি পৃষ্ঠচান্তয়োঃ পাশৌ প্রতিমূচ্য লক্ষণেন দক্ষিণাপায়স্য লক্ষণে শম্ভু নিহন্তি তদক্ষিণায়েরায়তনং ভবতি।”
এই শ্লোকগুলিকে যদি গণিতের ভাষায় আলোচনা করা যায় তাহলে নিম্নরূপ হবে:
এখানে A = আহ্বনীয়, G = গার্হপত্য, D = দক্ষিনাগ্নি ধরা হয়েছে
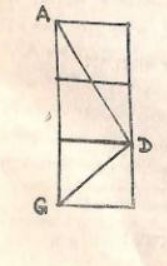
ধরা যাক AG = b তাহলে সূত্রানুযায়ী পাওয়া যায়
b b 16 18 b, AD=v5,6,7, 66, 6. 3 BD = b 3 v2, b b, 9 21 25 26, 76, 86, 51821 12/25 b
এবং এর ফলে পাওয়া যায় √5 × 5 =2 1 ^ 2 ,2 1 ^ 1 ,2 7 ^ 3 ,2 25 ^ 4 2’4, 2’333, 2285, 2.16. 2-12, 11166, 144.
বর্তমান গণনায় √5 = 2·23607 এবং √ 2 = 1· 414213 ･･････ পাওয়া যায়।
মানব শুষ সূত্রে অবশ্য 2 ইত্যাদি ছাড়াও
√29 5:3888. এবং √61 = 7 · 8333 মান দেওয়া হয়েছে।
একথা সত্য যে শুথ সূত্রে করণী নির্ণয় করার কোন নির্দিষ্ট নিয়ম বা পদ্ধতি উল্লেখ করা হয় নি। যে সূত্রসমূহ শুষস্থত্রে দেখা যায় তার উপর ভিত্তি করে প্রাচ্য ও পাশ্চাত্য পণ্ডিতেরা একটি নিয়ম খাড়া করেছেন।
(চলবে)
প্রাচীন ভারতে গণিতচর্চা (পর্ব-২২৭)
