প্রদীপ কুমার মজুমদার 
সমীকরণগুলির সমাধান করার জন্য বিস্তৃত আলোচনা শুষস্থত্রে দেখতে পাওয়া যায় না।
তৃতীয় ও পঞ্চম স্তর প্রথম স্তরের ন্যায় এবং চতুর্থ স্তর দ্বিতীয় স্তরের ন্যায় সাজান হল। এ থেকে নিম্নলিখিত সমীকরণ পাই-
এর দুটি মাত্র সমাধান পাওয়া যায় (ধনাত্মক পূর্ণ সংখ্যায়)
x = 5, y = 16, m = 3, n = 4 x = 9, y = 12, m = 6, n = 4
“গরুড় চয়ন চিতি” নির্মাণ করতে গিয়ে একটু কঠিন ধরনের একাধিক অজ্ঞাত রাশির অনির্ণেয় সমীকরণের সাক্ষাৎ মেলে।
বলা হয়েছে এটি ৭২ বর্গপুরুষ ক্ষেত্রফল বিশিষ্ট এবং ৫টি স্তরে বিভক্ত। সাজানোর ক্ষেত্রে প্রত্যেকটি স্তর পূর্ববর্তী বা পরবর্তী স্তর অপেক্ষা পৃথক। প্রত্যেকটি বস্তরে বিভিন্ন মাপের ২০০টি ইট থাকবে। মহর্ষি বৌধায়ণ চারটি বিভিন্ন মাত্রার ইটের কথা উল্লেখ করেছেন। এই আলোচনা থেকে নিম্নলিখিত সমীকরণদ্বয় পাওয়া যায়।
m, n, p এবং এ ধনাত্মক পূর্ণ সংখ্যা।
এখানে m, n, p এবং ৫ এর মান সমীকরণদ্বয় সমাধান করার পর পাওয়া যায় এবা মানগুলি হচ্ছে
m = 16 n = 25 p = 36 q = 100 ;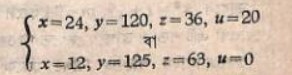 
এক্ষেত্রে পাঁচ ধরনের ইটের কথা মহর্ষি আপস্তম্ব বলছেন। প্রসঙ্গক্রমে বলা প্রয়োজন সমীকরণগুলির সমাধান করার জন্য বিস্তৃত আলোচনা শুষস্থত্রে দেখতে পাওয়া যায় না। আপস্তম্ব শুন সূত্রের বিভিন্ন ভান্তকার যেমন করবিন্দস্বামী, কপর্দিস্বামী ও সুন্দররাজ উপযুক্ত সমীকরণটির সমাধান বের করেছেন। তাঁদের সমাধানকৃত মানগুলি হচ্ছে এই
প্রসঙ্গক্রমে বলা প্রয়োজন যে মহর্ষি আপস্তম্ব পাঁচ ধরণের ইটের কথা উল্লেখ করেছেন। তাঁর সমাধান নিম্নলিখিত সমীকরণদ্বয় থেকে পাওয়া যায় x + y + z + w + u = 200.
অন্যান্য কতকগুলি যজ্ঞবেদী নির্মাণ করতে গিয়ে বিভিন্ন শুথস্থত্রে নিম্নলিখিত সমীকরণগুলির সাক্ষাৎ পাই।
এছাড়াও আরও নানাধরণের সমীকরণ বিভিন্ন শুণ সূত্রের মধ্যে দেখতে পাওয়া যায়।
(চলবে)
