প্রদীপ কুমার মজুমদার 
অজ্ঞাত রাশির ঘনবর্গের সঙ্গে সেই জাতীয় অজ্ঞাতরাশির ঘনবর্গ, অজ্ঞাতরাশির যড়ঘাতের সঙ্গে সেই জাতীয় অজ্ঞাতরাশির ষড়ঘাত যোগ বা বিয়োগ করতে হবে
এ থেকে বোঝা যে সে মহাবীরের সময় কাল্পনিক রাশির প্রচলন হয় নাই। কিন্তু দুটি বীজের কথা সে সময়ে তাঁরা জানতেন শ্রীপতি সিদ্ধান্ত শেখরের চতুর্দশ অধ্যায়ের পঞ্চম শ্লোকে বলেছেন-
ধনং ক্ষয়স্যাথ ধনস্ত বর্গৌ
তে এব মূলে তু তয়োর্ডবেতাম্।
ঋণক্ষ নো মূলমবর্গহেতো-
রিতখং ঘনশ্যাপি বিধিবিধেয়ঃ।
অর্থাৎ ঋণ বা ধনরাশির বর্গ ধনই হবে। ধনাত্মক বর্গরাশির মূল ধন।
……। ঋণাত্মক রাশির বর্গমূল নাই।
যেহেতু তাহা বর্গ নহে।
দ্বিতীয় ভাস্করাচার্য প্রায় একই কথা বলেছেন।
আধুনিক বীজগণিতে যদি α1x +17+7, এবং x+y+72 এই দুটি যোগ করতে হয় তাহলে প্রথমে আমরা লিখি
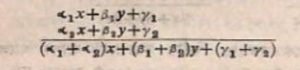
অর্থাৎ এ-এর তলেx; ৮-এর তলে y প্রভৃতি রেখে যোগ বা বিয়োগ করি। এ ধরণের সূত্র বা নিয়ম (যাই বলা হোক না কেন) ভারতীয় বীজগণিতে দেখা যায়।
যেমন ব্রাহ্মস্ফুট সিদ্ধান্তের অষ্টাদশ অধ্যায়ের ৪১ তম শ্লোকে বলা হয়েছে
অব্যক্তবর্গ ঘনবর্গ বর্গপঞ্চগত ষড়,গতাদীনাম।
তুল্যানাং সংকলিত ব্যবকলিত পৃথগতুল্যানাম্।
অর্থাৎ অজ্ঞাত রাশির বর্গের সঙ্গে সেই জাতীয় অজ্ঞাত রাশির বর্গ, অজ্ঞাত রাশির ঘনবর্গের সঙ্গে সেই জাতীয় অজ্ঞাতরাশির ঘনবর্গ, অজ্ঞাতরাশির যড়ঘাতের সঙ্গে সেই জাতীয় অজ্ঞাতরাশির ষড়ঘাত যোগ বা বিয়োগ করতে হবে।..
দ্বিতীয় ‘ভাস্করাচার্য বলেছেন-
“যোগোহন্তরং তেষু সমানজাত্যোবিভিন্ন জাত্যোশ্চ পৃথক্ স্থিতিশ্চ।”
একই জাতের অজ্ঞাতরাশির সঙ্গে একই জাতের অজ্ঞাতরাশির যোগ বা বিয়োগ করবে।
(চলবে)
প্রাচীন ভারতে গণিতচর্চা (পর্ব-২৮১)
