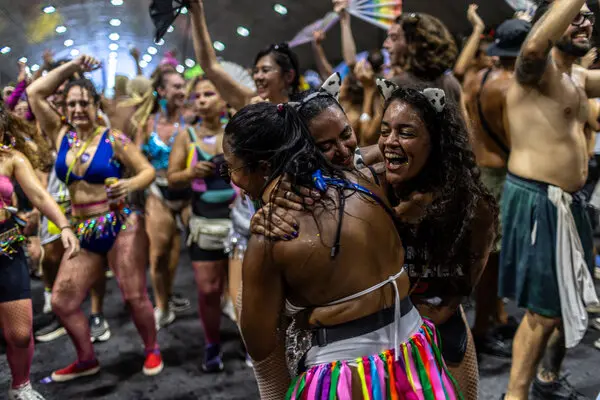প্রদীপ কুমার মজুমদার 
সেই তিনটি রাশি অপরের অংশদ্বয়ের দ্বারা বিযুক্ত হয়ে ৬০ শেষ হয়।
দ্বিতীয় পদ্ধতি:- (i) নং সমীকরণ থেকে পাওয়া যায় x=2y-300.
(গ) অনেক অজ্ঞাত রাশি বিশিষ্ট একমাত্রার সমীকরণ বাকশালীর পাণ্ডুলিপি, প্রথম আর্যভটের আর্যভটীয়, ব্রহ্মগুপ্তের ব্রাহ্মস্ফুট সিদ্ধান্ত, মহাবীরের গণিতসার সংগ্রহ, দ্বিতীয় ভাস্করাচার্যের বীজগণিত প্রভৃতি গ্রন্থে দেখা যায়। এই ধরণের সমীকরণ নানা প্রকার এবং নানা পদ্ধতিতে সমাধান করা যায় সে কথা অধিকাংশ ভারতীয় গণিতবিদ বলে গিয়েছেন।
প্রসঙ্গত বলা প্রয়োজন দত্ত এবং সিংহের হিস্ত্রী অব হিন্দু ম্যাথেমেটিকসে এ নিয়ে ব্যাপক আলোচনা করা হয়েছে।২ আমি এখানে দ্বিতীয় ভাস্করাচার্যের বীজগণিত থেকে একটি উদাহরণ তুলে ধরলাম।
সার্ভপফাংশনবমৈযুক্তাঃ কে স্থ্যঃসমান্বয়ঃ। অন্যাংশন্বয়হীনাশ্চ যষ্টিশেযাশ্চ তান বদ।
অর্থাৎ কোন তিনটি রাশি নিজের অর্ধেক, নিজের পঞ্চমাংশ, এবং নিজের নবমাংশ যুক্ত হয়ে সমান হয়। সেই তিনটি রাশি অপরের অংশদ্বয়ের দ্বারা বিযুক্ত হয়ে ৬০ শেষ হয়।
উদাহরণটিকে বীজগণিতের ভাষায় প্রকাশ করলে দাঁড়ায়’
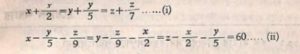
দ্বিতীয় ভাস্করাচার্য এটি সমাধান এইভাবে করেছেন-
অস্ত্র সমরাশিমানং যা ১। ততো বিলোম-বিধিনা অথ স্বাংশাধিকোন ইত্যাদিনা রাশয়ঃ যা উ, যাওঁ, যা ।
এতে অন্যভাগদ্বয়েনীনাঃ সর্বেংহপ্যেবং শেষাঃ স্ন্যঃ যাই। এতত যর্ভিসমং রুত্বাপ্ত-যাবত্তাবন্নানেন ১৫০। উত্থাপিতাঃ জাতারাশয়ঃ ১০০। ১২৫। ১৩৫।
অর্থাৎ যা = ৮ ধরলে আমরা সমাধানটির আধুনিক রূপ হয় এইরূপ-
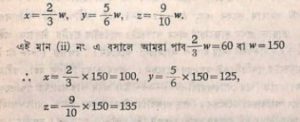
প্রসঙ্গত বলা প্রয়োজন, যে এ ছাড়া আরও নানা ধরণের উদাহরণ বিভিন্ন গণিত গ্রন্থে দেখা যায়।
(চলবে)
প্রাচীন ভারতে গণিতচর্চা (পর্ব-২৯০)
